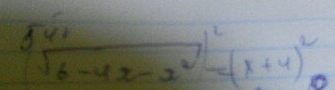Научите решать подобные уравнения

Корень в степени 2 в левой части можно убрать, так как 1/2 * 2 = 1
Квадрат суммы раскрываем так: (x+4)² = x² + 8x + 16

6 - 4x - x² = x² + 8x + 16
2x² + 12x + 10 = 0

Найдем дискриминант:
D = b²-4ac
D = (12)² - 4*2* 10 = 144 - 80 = 64

x₁= (-b+√D)/2a;
x₁ = (-12 + √64) / 2*12 = (-12 + 8) / 24 = - 4/24 = -1/6

x₂= (-b-√D)/2a
x₂ = (-12 - √64) / 2*12 = (-12 - 8) / 24 = -20/24 = -5/6

Решим подкоренное выражение:
6 - 4x - x² >= 0
6 - 4x - x² = 0

Найдем дискриминант:
D = b²-4ac
D = (-4)² - 4*-1* 6 = 16 + 24 = 40

x₁= (-b+√D)/2a;
x₁ = (4 + √40) / 2*-1 = (4 + 6,3) / -2 = - 5,15

x₂= (-b-√D)/2a
x₂ = (4 - √40) / 2*-1 = (4-6,3) / -2 = 1,15

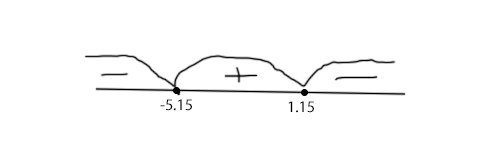
Смотри рисунок снизу и проверяем входят ли корни:
-1/6 входит в интервал с плюсом
-5/6 входит в интервал с плюсом

оба корня подходят