1) Точка M не лежит в плоскости параллелограмма ABCD. На отрезке AM выбрана точка E так, что ME:EA=2:3

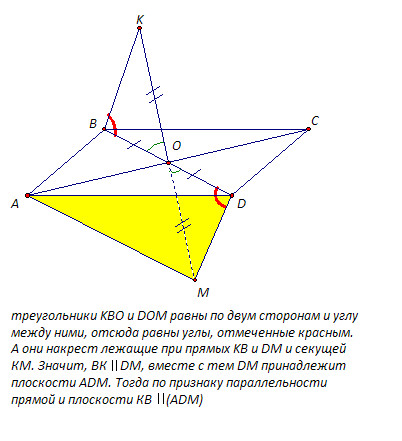
Задача №1
Согласно условию отрезок АМ вертикален, следовательно плоскость МАВ тоже вертикальна.

В плоскости СDE проведем отрезок ЕВ1 параллельный и равный АВ. Он одновременно находится в плоскости СDE и в вертикальной плоскости МАВ. Поэтому точка F пересечения отрезка МВ с плоскостью СDE находится на пересечении отрезков МВ и ЕВ1.

В плоскости МАВ находится два подобных треугольника: MEF и FF1B ( точка F1 -это проекция точки F на АВ).

Отрезок FF1 равен ЕА.
Поэтому F1B = (3/2)*10 = 15 см.
АF1 = ЕF = 10 см.
Отсюда АВ = 10+15 = 25 см.

Однако, такое решение является частным случаем, поскольку где бы ни находилась точка М, ∆MFE и ∆AMB остаются подобными, отношение ЕF:AB=2:5, и АВ получается равным 25 см.

Задача №2

Треугольники KBO и DOM равны по двум сторонам и углу между ними. Поэтому углы отмеченные красным равны. Они являются накрест лежащими при прямых KB и DM и секущей KM. Значит, BK || DM, вместе c тем DM принадлежит плоскости ADM. Тогда по признаку параллельности прямой и плоскости KB || ADM